 |
21. Основные понятия динамикиПервый закон Ньютона Проделаем опыт. Тележку на колесиках скатим с наклонной плоскости на пол, где насыпана горка песка. Доехав до нее, тележка увязнет в песке и остановится. Разровняем песок и вновь позволим тележке съехать с горки. Теперь скорость тележки будет уменьшаться гораздо медленнее. Если же убрать песок, то уменьшение скорости тележки и вовсе будет едва заметно. На основе этих наблюдений можно сформулировать следующее обобщение: всякое тело, свободное от воздействия других тел, сохраняет свою скорость неизменной. Это утверждение называется первым законом Ньютона и означает следующее. Если тело движется с некоторой скоростью, то оно и будет продолжать двигаться с той же скоростью до тех пор, пока действие другого тела не заставит его изменить либо быстроту, либо направление движения. Если же тело покоится (то есть скорость равна нулю), то оно и будет продолжать покоиться (то есть скорость останется прежней) до тех пор, пока действие другого тела не заставит его прийти в движение. Однако тележка, едущая по полу, все же не является "телом, свободным от воздействия других тел", о котором говорится в законе. На тележку действуют Земля (сила тяжести) и пол (сила упругости). Чтобы завершить наш эксперимент, нам нужно "убрать" и эти силы. Для этого поместим тележку в космический корабль и перелетим на поверхность Марса. Там сила тяжести заметно меньше, чем на Земле. Вес тележки, а, значит, и сила ее давления на колеса уменьшится, следовательно, уменьшится сила трения в осях колес. Теперь скорость тележки, съехавшей с горки, будет уменьшаться еще медленнее. Перелетим с Марса на Луну. Сила тяжести, вес тележки и сила трения в осях ее колес станут еще меньше. И если их удалить вообще, то тележка, как и любое другое свободное тело будет вечно сохранять свою скорость постоянной. Движение свободного тела называют движением по инерции, а сохранение им скорости называют явлением инерции. Вспомним, однако, что скорость тела – это не свойство самого тела. Скорость может быть разной с точки зрения разных наблюдателей (см. § 13-е). Другими словами, можно найти такую систему отсчета, в которой свободное тело не будет сохранять свою скорость. Например, если в тот момент, когда тележка едет по полу космического корабля, включить его двигатели и начать взлетать, то тележка с невероятной скоростью покатится к хвостовой его части. Таким образом, во взлетающем корабле первый закон Ньютона не выполняется. Забегая вперед, скажем, что в этом случае не выполняются и второй, и третий законы Ньютона. Именно для того и нужен первый его закон, чтобы определить, можно ли в данной системе отсчета пользоваться остальными законами Ньютона. Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными системами отсчета. Для изучения движения людей, автомобилей, самолетов систему отсчета "наблюдатель на Земле" вполне можно считать инерциальной системой. Расчеты, сделанные в ней на основе второго закона Ньютона, довольно точно описывают движения этих тел. Второй закон Ньютона В 7 классе мы познакомились с силой – физической величиной, измеряемой прибором динамометром и характеризующей действие одного тела на другое. Мы также узнали, что если на тело действует неуравновешенная сила, то такое тело обязательно изменяет свою скорость или направление движения (см. § 3-г). Другими словами, действие на тело неуравновешенной силы приводит к появлению ускорения. В 9 классе мы научились измерять и ускорения. Для этого служат специальные формулы (см. § 13-л, 13-м). Возникает вопрос: каким образом сила и вызываемое ей ускорение связаны друг с другом? Какова формула, выражающая связь этих величин? Ответ на этот вопрос дает второй закон Ньютона: вектор силы, действующей на тело, в инерциальной системе отсчета равен произведению массы на вектор ускорения этого тела. Чтобы убедиться в справедливости этой формулы, нужно измерить величины F и ma по отдельности, а затем сравнить их численные значения и направления векторов. Сделаем это. Возьмем прибор, представляющий из себя легко вращающийся диск (1). На нем укреплены указатель частоты вращения (2) и толстая линейка (3), одновременно служащая "рельсом" для ролика (4). При помощи нити ролик привязан к динамометру (5). При вращении ролик натянет нить, и динамометр покажет некую силу F, тем бо'льшую, чем быстрее вращается диск. Вращая диск, мы получим, например, такие данные: | | Ролик массой 0,25 кг | Ролик массой 0,5 кг | | радиус (R), м | 0.2 | 0.2 | 0.2 | 0.2 | | период (T), с | 1 | 2 | 1 | 2 | | ускорение (а) | » 8 м/с2 | » 2 м/с2 | » 8 м/с2 | » 4 м/с2 | | сила (F) | »2 H | »0.5 H | »4 H | »1 H |
Рассмотрим, как получились эти числа. Радиус R – это расстояние от ролика до центра диска. Во время вращения диска ролик откатывается по линейке до отметки 20 см. Значит, R = 0.2 м. Период T – это время, за которое диск совершает один оборот. Указатель частоты вращения на рисунке показывает 1 об/с. То есть за секунду совершается один оборот. Следовательно, период T = 1 с. Вычисляя центростремительное ускорение ролика по формуле a = 4p2R/T2 (см. § 13.13), получим: 4 · 3.142 · 0.2 / 12 » 8 м/с2. Именно это число и записано в клетке "ускорение". Итак, справедливо ли равенство F=ma? Перемножим подчеркнутые числа верхней таблицы. Имеем: 2 Н » 0.25 кг · 8 м/с2. Другими словами, F » ma. Теперь убедимся, что векторы F и ma сонаправлены. Вспомним, что вектор центростремительного ускорения тела при его равномерном движении по окружности всегда направлен к центру этой окружности. Выясним, куда направлен вектор силы, придающей ролику это ускорение. Вообразим на мгновение, что нить, связывающая ролик и динамометр, вдруг оборвалась. Что произойдет с роликом? Он покатится по линейке и соскочит с диска. Следовательно, нить тянула ролик к оси вращения, не позволяя ему откатиться дальше. Другими словами, вектор F сонаправлен с вектором ускорения. Таким образом мы подтвердили истинность векторного равенства: F = ma. Третий закон Ньютона Первый закон Ньютона говорит нам, что в некоторых системах отсчета у тела нет ускорения, если на него не действуют другие тела. Второй закон Ньютона развивает сказанное. Он говорит уже о том, какое именно ускорение появляется у тела (в той же системе отсчета), если на него начнут действовать другие тела. А третий закон Ньютона говорит нам уже о том, что происходит с теми телами, под действием которых находится рассматриваемое нами тело: | F12 = – F21 | F12 – | сила действия первого тела на второе | | F21 – | сила действия второго тела на первое |
Словами третий закон Ньютона звучит: взаимодействующие тела действуют друг на друга с силами, векторы которых равны по величине и противоположны по направлению. Приведем пример. Мы знаем, что на Луну действует сила тяготения Земли. Поэтому, согласно формуле F=ma, Луна имеет центростремительное ускорение и обращается по орбите вокруг Земли. Но, согласно формуле F12 = F21, и Луна должна действовать на Землю, причем с такой же силой. Невероятно, но факт! Ученые выяснили, что Луна обращается не вокруг Земли, а вокруг некоторой точки, называемой центром масс системы Луна-Земля (обозначена желтым цветом). Удивительно, но и Земля обращается вокруг этой же точки! Таким образом, не только Луна, но и Земля имеет центростремительное ускорение. Значит, согласно второму закону Ньютона, на Землю действует некоторая сила, вызывающая это ускорение. Эта сила – именно сила тяготения Луны, поскольку оба небесных тела обращаются вокруг одной и той же точки. Таким образом мы подтвердили часть третьего закона Ньютона: оба взаимодействующих тела действуют друг на друга. Закон всемирного тяготения Закон всемирного тяготения был открыт англичанином И. Ньютоном в 1666г. Закон звучит следующим образом: сила гравитационного притяжения двух материальных точек прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. В виде формулы это записывается так: 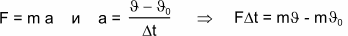 | m1, m2 – | массы взаимодействующих материальных точек, кг | | r – | расстояние между ними, м | | G – | коэффициент, » 6.7·10-11 Н·м2/кг2 |
Убедиться в справедливости этой формулы нам поможет… Луна. Известно, что ее орбита почти круговая, и Луна делает один оборот за 27.3 суток. Известно также, что радиус орбиты Луны примерно в 60 раз больше радиуса Земли и составляет » 384 тыс км. Рассчитаем центростремительное ускорение Луны: 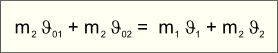
В § 13.11 мы выяснили, что вблизи Земли все тела, свободно летящие вниз или как угодно иначе, имеют одинаковое ускорение: 9.8 м/с2. Поделив это число на подсчитанное нами значение aл, мы получим » 3600 или » 602. То есть ускорение тел, свободно летящих вблизи Земли, в 602 раз больше ускорения тел, летающих на расстояниях, в 60 раз более далеких (как, например, Луна). Вспомним, что ускорение свободного падения не зависит от массы тел. Значит, ускорение любого тела, удаленного от Земли на расстояние Луны, будет равно ускорению самой Луны. Тогда, согласно второму закону Ньютона, сила тяготяния этого тела к Земле на Земле тоже будет в 602 раз больше силы тяготения этого же тела к Земле на Луне. Таким образом мы убедились в справедливости второй части закона всемирного тяготения: сила тяготения между телами, обратно пропорциональна квадрату расстояния между ними.
Импульс тела и импульс силы
Проведем простое наблюдение. Положим на стол теннисный шарик. Если на него подуть, то шарик немного откатится в сторону. Если подуть сильнее, то шарик откатится дальше. Такого же результата можно достичь, если дуть не сильно, но более длительное время. Другими словами, результат действия силы на тело зависит не только от самой силы, но и от времени ее действия. Произведение силы на время ее действия называется импульсом силы: 
Проведем мысленный эксперимент. Вообразим, что у нас есть тележка с песком, стоящая на рельсах. Выстрелим из пистолета в тележку так, чтобы пуля застряла в песке. В результате тележка покатится по рельсам. Остановим ее и возьмем тяжелую гирю. Пронося ее над тележкой с небольшой скоростью, уроним на песок. После нескольких тренировок гирю можно уронить так, чтобы тележка двигалась с такой же скоростью, как и после выстрела из пистолета. В этом случае говорят, что пуля и гиря передали тележке одинаковое количество движения. Пуля имела маленькую массу, но большую скорость. Гиря же имела маленькую скорость, но большую массу. Следовательно, количество движения тела зависит от его массы и скорости. Количеством движения или импульсом тела называют произведение массы тела на вектор его скорости: 
Поскольку скорость – векторная величина, а масса – положительный скаляр, то импульс тела, mJ – вектор, сонаправленный с вектором скорости. Закон сохранения импульса Подставим в формулу второго закона Ньютона формулу определения ускорения. В результате получим: 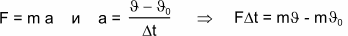 Обратите внимание, что в левой части равенства мы получили уже знакомую нам величину FDt – импульс силы. В правой части равенства тоже стоят знакомые нам величины: mJ – конечный импульс и mJ0 – начальный импульс тела. Разность mJ – mJ0 представляет собой изменение импульса тела. Поэтому полученную нами формулу мы прочтем так: импульс силы равен изменению импульса тела. Рассмотрим два взаимодействующих тела, например, бильярдные шары. Запишем для них формулу третьего закона Ньютона F1 = – F2 и выведенную нами формулу: F1Dt = m1J1 – m1J01 и F2Dt = m2J2 – m2J02 Подставив два последних равенства в формулу третьего закона Ньютона и проведя преобразования, получим: 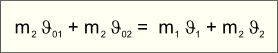 Это утверждение называют законом сохранения импульса: сумма импульсов тел до взаимодействия равна сумме их импульсов после взаимодействия. Однако закон справедлив лишь в том случае, если рассматриваемые тела взаимодействуют только друг с другом. Быстро летящие бильярдные шары можно приблизительно считать взаимодействующими только друг с другом. Поэтому на чертеже выполяется векторное равенство: 5 м/с = 3 м/с + 4 м/с . Учебник "Физика-9" Кривченко И.В.
|
 |


